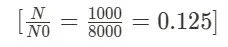GCSE Physics Tutorial - Determining the Half-Life of a Radioactive Isotope
In this tutorial, we will learn how to determine the half-life of a radioactive isotope from given information. The half-life is a fundamental property that describes the decay rate of unstable atomic nuclei. Understanding how to calculate the half-life is crucial in nuclear physics and radiometric dating. Let's delve into the steps involved in determining the half-life of a radioactive isotope.
Steps to Determine the Half-Life of a Radioactive Isotope:
Gather Given Information: Collect all the relevant information provided in the problem. This may include the initial number of radioactive nuclei (N0), the remaining number of radioactive nuclei (N), and the time elapsed (t) between the initial measurement and the current measurement.
Calculate the Fraction of Remaining Nuclei: The fraction of remaining nuclei ($ \frac{N}{N0} )$ is obtained by dividing the number of remaining nuclei (N) by the initial number of nuclei (N0).
Calculate the Decay Constant (λ): The decay constant (λ) is a constant unique to each radioactive isotope and determines the probability of decay per unit time. It can be calculated using the formula: $[ \lambda = \frac{-\ln(\frac{N}{N0})}{t} ]$
Calculate the Half-Life (t½): The half-life (t½) can be determined using the decay constant (λ) with the formula: $[ t_{1/2} = \frac{\ln(2)}{\lambda} ]$
Round the Result: Round the calculated half-life to an appropriate number of significant figures based on the given data and the level of accuracy required.
Example: Let's work through an example to determine the half-life of a hypothetical radioactive isotope:
Suppose an initial sample contains 8000 radioactive nuclei. After 10 days, the number of remaining nuclei is 1000.
Given information:
N0 (Initial number of nuclei) = 8000
N (Remaining number of nuclei) = 1000
t (Time elapsed) = 10 days
Step 1: Calculate the Fraction of Remaining Nuclei:
Step 2: Calculate the Decay Constant (λ):
Step 3: Calculate the Half-Life (t½):
Step 4: Round the Result: The half-life of the radioactive isotope is approximately 3.01 days.
In this tutorial, we have learned how to determine the half-life of a radioactive isotope using given information. By calculating the fraction of remaining nuclei and the decay constant, we can find the half-life of the isotope. This knowledge is valuable in radiometric dating and helps us understand the decay rate of radioactive isotopes, which is essential in various fields of science and technology.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!