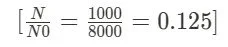GCSE Physics Tutorial - Calculating Net Decline Ratio in Radioactive Emission
In this tutorial, we will learn how to calculate the net decline ratio in a radioactive emission after a given number of half-lives. When a radioactive substance undergoes decay, its population of radioactive nuclei decreases over time. The net decline ratio provides a way to express the reduction in the number of radioactive nuclei as a ratio compared to the initial number. Understanding this concept is essential in radiometric dating and studying the behaviour of radioactive materials. Let's explore how to calculate the net decline ratio.
Steps to Calculate Net Decline Ratio:
Gather Given Information: Collect all the relevant information provided in the problem. This includes the initial number of radioactive nuclei ($N_0$), the remaining number of radioactive nuclei (N), and the number of half-lives that have elapsed (n).
Calculate the Fraction of Remaining Nuclei: The fraction of remaining nuclei ( $ \frac{N}{N_0} $ ) is obtained by dividing the number of remaining nuclei (N) by the initial number of nuclei ($N_0$).
Calculate the Net Decline Ratio: The net decline ratio expresses the reduction in the number of radioactive nuclei as a ratio to the initial number. It can be calculated using the formula: $ [ \text{Net Decline Ratio} = \frac{N}{N_0} = \left( \frac{1}{2} \right)^n ] $
Convert the Ratio to Percentage (Optional): If required, the net decline ratio can be expressed as a percentage by multiplying it by 100. This step helps in better understanding the magnitude of the decline.
Example: Let's work through an example to calculate the net decline ratio in a radioactive emission after a given number of half-lives:
Suppose an initial sample contains 6400 radioactive nuclei. After 4 half-lives, the number of remaining nuclei is 400.
Given information:
$N_0$ (Initial number of nuclei) = 6400
N (Remaining number of nuclei) = 400
n (Number of half-lives elapsed) = 4
Step 1: Calculate the Fraction of Remaining Nuclei: $[ \frac{N}{N_0} = \frac{400}{6400} = 0.0625 ]$
Step 2: Calculate the Net Decline Ratio: $[ \text{Net Decline Ratio} = \left( \frac{1}{2} \right)^4 = 0.0625 ]$
Step 3: Convert the Ratio to Percentage (Optional): The net decline ratio is 0.0625, which can be expressed as 6.25% (0.0625 x 100%).
In this tutorial, we have learned how to calculate the net decline ratio in a radioactive emission after a given number of half-lives. By determining the fraction of remaining nuclei and applying the concept of halving during each half-life, we can express the net decline as a ratio compared to the initial number. The net decline ratio provides valuable information about the reduction in radioactive nuclei over time and is an essential tool in radiometric dating and studying radioactive materials.
To calculate the net decline ratio (NDR) using the half-life of a radioactive substance, you can use the formula:
$ \text{NDR} = \left( \frac{1}{2} \right) ^{ \frac{t}{T_{ \frac{1}{2}}}}$
Where:
$ \text{t}$ = Time elapsed
$ \text{T}_{ \frac{1}{2}}$ = Half-life of the radioactive substance
For example, let's say the half-life of a radioactive substance is 5 years, and 10 years have passed. To find the net decline ratio:
$ \text{NDR} = \left( \frac{1}{2} \right)^{ \frac{10}{5}} = \left( \frac{1}{2} \right)^2 = \frac{1}{4}$
So, the net decline ratio is $ \frac{1}{4}$ or 0.25.
This means that after 10 years, only 25% of the original radioactive substance remains.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - Determining the Half-Life of a Radioactive Isotope
In this tutorial, we will learn how to determine the half-life of a radioactive isotope from given information. The half-life is a fundamental property that describes the decay rate of unstable atomic nuclei. Understanding how to calculate the half-life is crucial in nuclear physics and radiometric dating. Let's delve into the steps involved in determining the half-life of a radioactive isotope.
Steps to Determine the Half-Life of a Radioactive Isotope:
Gather Given Information: Collect all the relevant information provided in the problem. This may include the initial number of radioactive nuclei (N0), the remaining number of radioactive nuclei (N), and the time elapsed (t) between the initial measurement and the current measurement.
Calculate the Fraction of Remaining Nuclei: The fraction of remaining nuclei ($ \frac{N}{N0} )$ is obtained by dividing the number of remaining nuclei (N) by the initial number of nuclei (N0).
Calculate the Decay Constant (λ): The decay constant (λ) is a constant unique to each radioactive isotope and determines the probability of decay per unit time. It can be calculated using the formula: $[ \lambda = \frac{-\ln(\frac{N}{N0})}{t} ]$
Calculate the Half-Life (t½): The half-life (t½) can be determined using the decay constant (λ) with the formula: $[ t_{1/2} = \frac{\ln(2)}{\lambda} ]$
Round the Result: Round the calculated half-life to an appropriate number of significant figures based on the given data and the level of accuracy required.
Example: Let's work through an example to determine the half-life of a hypothetical radioactive isotope:
Suppose an initial sample contains 8000 radioactive nuclei. After 10 days, the number of remaining nuclei is 1000.
Given information:
N0 (Initial number of nuclei) = 8000
N (Remaining number of nuclei) = 1000
t (Time elapsed) = 10 days
Step 1: Calculate the Fraction of Remaining Nuclei:
Step 2: Calculate the Decay Constant (λ):
Step 3: Calculate the Half-Life (t½):
Step 4: Round the Result: The half-life of the radioactive isotope is approximately 3.01 days.
In this tutorial, we have learned how to determine the half-life of a radioactive isotope using given information. By calculating the fraction of remaining nuclei and the decay constant, we can find the half-life of the isotope. This knowledge is valuable in radiometric dating and helps us understand the decay rate of radioactive isotopes, which is essential in various fields of science and technology.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - Half-Life and Its Relation to the Random Nature of Radioactive Decay
In this tutorial, we will explore the concept of half-life and how it is related to the random nature of radioactive decay. The half-life of a radioactive isotope is a fundamental property used to describe the decay rate of unstable atomic nuclei. Understanding the relationship between half-life and the random nature of decay is crucial in nuclear physics and radiometric dating. Let's delve into the concept of half-life and how it is influenced by the random behaviour of radioactive decay.
Definition of Half-Life: The half-life of a radioactive isotope is the time it takes for half of the original number of radioactive nuclei in a sample to decay. It is a characteristic property of each radioactive isotope and remains constant over time, regardless of the size of the sample. The concept of half-life is used to describe the exponential decay of radioactive nuclei in a given sample.
Random Nature of Radioactive Decay: Radioactive decay is a random process that occurs at the level of individual atomic nuclei. Unstable atomic nuclei transform into more stable configurations by emitting various types of radiation, such as alpha particles, beta particles, or gamma rays. The timing of decay for an individual nucleus is unpredictable and not influenced by external factors.
Influence of Half-Life on Decay Rate: The half-life of a radioactive isotope is related to the probability of decay for each individual nucleus in the sample. The decay process is probabilistic, meaning that each nucleus has a certain probability of decaying within a specific time interval.
Predicting Individual Decay Times: Due to the random nature of decay, it is not possible to predict when an individual nucleus will decay. However, we can make statistical predictions about the behaviour of a large group of radioactive nuclei. For example, after one half-life, on average, half of the radioactive nuclei in the sample will have decayed.
Consistency of Half-Life: Despite the random nature of decay, the half-life of a radioactive isotope remains constant over time. It does not change based on the number of remaining nuclei or external conditions. This consistency allows scientists to use the concept of half-life to estimate the age of rocks, fossils, and artifacts in radiometric dating.
Half-Life and Radioactive Dating: In radiometric dating, scientists measure the remaining amount of a radioactive isotope in a sample and compare it to the initial amount. By knowing the half-life of the isotope, they can determine the time that has elapsed since the sample was formed.
In this tutorial, we have explored the concept of half-life and its relation to the random nature of radioactive decay. The half-life of a radioactive isotope is the time it takes for half of the radioactive nuclei in a sample to decay, and it remains constant over time. The random nature of decay makes it impossible to predict the exact timing of individual decays, but statistical predictions can be made for a large group of nuclei. Understanding the concept of half-life is essential for radiometric dating and provides valuable information about the decay rate of radioactive isotopes.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - The Half-Life of Radioactive Isotopes
In this tutorial, we will explore the concept of the half-life of a radioactive isotope. The half-life is a fundamental characteristic of radioactive decay and is defined as the time it takes for the number of isotope nuclei in a sample to halve. Understanding the half-life is crucial in nuclear physics and has practical applications in radiometric dating and the study of radioactive materials. Let's delve into the definition and significance of the half-life of radioactive isotopes.
Definition of Half-Life: The half-life of a radioactive isotope is the time required for half of the original number of radioactive nuclei in a sample to decay. It is a characteristic property of each radioactive isotope and remains constant over time, regardless of the size of the sample.
Decay and Half-Life: During radioactive decay, unstable atomic nuclei transform into more stable configurations by emitting radiation. The decay process follows an exponential decay curve. Each isotope has a specific half-life, which determines the rate at which its radioactive nuclei decay.
Representing Half-Life: Half-life is usually denoted by the symbol $ t_{1/2} $. It is the time interval in which half of the radioactive nuclei in the sample have decayed. After one half-life, the number of radioactive nuclei remaining in the sample is reduced by half.
Example of Half-Life: Suppose we have a sample of a radioactive isotope with a half-life of 10 minutes. If we start with 1000 nuclei at the beginning, after 10 minutes, 500 nuclei will remain. After another 10 minutes (20 minutes in total), only 250 nuclei will remain, and so on.
Half-Life is Independent of Sample Size: The half-life of a radioactive isotope remains constant regardless of the size of the sample. Whether the sample contains a large number of radioactive nuclei or just a few, the time taken for half of the nuclei to decay remains the same.
Applications of Half-Life: a. Radiometric Dating: By measuring the remaining amount of a radioactive isotope and knowing its half-life, scientists can estimate the age of rocks, fossils, and artifacts. This method is used in archaeology, geology, and paleontology. b. Medical Applications: In nuclear medicine, the half-life of radioactive isotopes is used to determine the appropriate dosage and timing for medical imaging and radiation therapy. c. Nuclear Power: Understanding the half-life of radioactive isotopes is essential for managing and safely disposing of nuclear waste generated in nuclear power plants.
In this tutorial, we have explored the concept of the half-life of radioactive isotopes. The half-life is the time it takes for half of the radioactive nuclei in a sample to decay, and it remains constant for each isotope. Understanding the half-life is crucial for various applications in radiometric dating, medical imaging, and nuclear power. The half-life provides valuable information about the decay rate of radioactive isotopes and plays a significant role in the study of nuclear processes.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - The Random Nature of Decay
In this tutorial, we will explore the concept that radioactive decay is random. Radioactive decay is a natural process in which unstable atomic nuclei transform into more stable configurations by emitting various types of radiation. Understanding that decay is a random process is crucial in nuclear physics and has practical implications in radiometric dating, medical imaging, and nuclear energy. Let's delve into why radioactive decay is considered a random phenomenon.
The Nature of Unstable Nuclei: Unstable atomic nuclei are characterised by having an excess of either protons or neutrons, making them energetically unstable. As a result, these nuclei are subject to radioactive decay to attain a more stable configuration.
The Decay Process: During radioactive decay, an unstable nucleus may undergo alpha decay ($ \alpha $), beta-minus decay ($ \beta^- $), beta-plus decay ($ \beta^+ $), gamma decay ($ \gamma $), electron capture ($ \text{EC} $), or positron emission ($ \text{β}^+ $). The type of decay and the time at which it occurs are unpredictable and random.
No External Influence: The decay of an unstable nucleus is not influenced by external factors such as temperature, pressure, or the presence of other particles. Each unstable nucleus has its own probability of decay, regardless of its surroundings.
Half-Life: The concept of half-life is used to describe the average time it takes for half of the radioactive nuclei in a sample to decay. However, it is important to note that the decay of individual nuclei is entirely random and not predictable.
Example of Random Decay: Imagine a sample of radioactive nuclei with a half-life of one hour. After the first hour, on average, half of the nuclei will have decayed. However, it is impossible to predict which individual nuclei will decay within that hour or when a specific nucleus will decay next.
Predicting Decay Times: Due to the random nature of decay, it is not possible to predict the exact time when an individual nucleus will decay. Nevertheless, we can make statistical predictions about the behaviour of a large group of radioactive nuclei.
Applications and Implications: The random nature of decay has practical applications in various fields. In radiometric dating, scientists can estimate the age of rocks and fossils by measuring the remaining amounts of certain radioactive isotopes. Additionally, in medical imaging and radiation therapy, understanding the random nature of decay is important for ensuring safe and effective practices.
In this tutorial, we have explored the concept that radioactive decay is a random process. Unstable atomic nuclei undergo decay in a probabilistic manner, independent of external influences. The random nature of decay is a fundamental aspect of nuclear physics and has significant applications in fields such as radiometric dating, medical imaging, and nuclear energy. Understanding this concept helps us interpret decay processes accurately and make informed decisions in various scientific and practical scenarios.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!