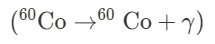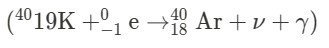GCSE Physics Tutorial - The Emission of Gamma Rays and Conservation of Mass and Charge
In this tutorial, we will explore the emission of gamma rays and how it does not cause the mass or charge of the nucleus to change. Gamma rays are high-energy electromagnetic waves emitted from the nucleus of an atom during gamma decay, a type of radioactive decay. Understanding this concept is important in nuclear physics to grasp the conservation of mass and charge during nuclear processes. Let's delve into why the emission of gamma rays does not affect the mass or charge of the nucleus.
Gamma Decay and Emission of Gamma Rays: Gamma decay is a process in which an excited atomic nucleus transitions to a lower energy state by releasing high-energy gamma rays. Unlike alpha and beta decay, gamma decay does not involve the emission of particles or cause the nucleus to change its identity. Instead, the nucleus emits a gamma ray (a photon of electromagnetic radiation) to release excess energy and reach a more stable state.
Mass Conservation: The emission of gamma rays during gamma decay does not alter the number of protons or neutrons in the nucleus. Therefore, the total mass of the nucleus remains unchanged before and after the emission of gamma rays. The mass number (A) of the parent nucleus is the same as the mass number of the daughter nucleus, indicating mass conservation.
Charge Conservation: Gamma decay does not involve the emission or absorption of charged particles (protons or electrons). As a result, the total charge of the nucleus remains unaffected during gamma decay. The parent nucleus and the daughter nucleus have the same number of protons (atomic number, Z), ensuring charge conservation.
Energy Conservation: Gamma decay is primarily driven by the need for the nucleus to reach a more stable energy state. The excess energy within the nucleus is released in the form of a gamma ray without altering the nucleus's identity or charge.
Representation in Decay Equations: Gamma decay is represented in decay equations as follows: \[ \text{Parent Nucleus} \rightarrow \text{Daughter Nucleus} + \gamma \]
In this tutorial, we have explored the emission of gamma rays during gamma decay and how it does not change the mass or charge of the nucleus. Gamma rays are high-energy electromagnetic waves emitted to release excess energy, allowing the nucleus to reach a more stable state. Mass and charge conservation are maintained throughout gamma decay, ensuring that the identity and charge of the nucleus remain the same. Understanding this concept is fundamental in nuclear physics and helps us comprehend the principles of energy conservation in radioactive decay processes.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - Balancing Radioactive Decay Equations
Introduction: In this tutorial, we will learn how to balance radioactive decay equations. Radioactive decay equations represent the process by which unstable atomic nuclei transform into more stable configurations by emitting various types of radiation. Balancing these equations is crucial in nuclear physics to ensure that the total mass number (A) and atomic number (Z) are conserved on both sides of the equation. Balancing radioactive decay equations correctly allows us to accurately represent the decay process and understand the transformations of unstable nuclei. Let's delve into the key steps for balancing radioactive decay equations.
Steps to Balance Radioactive Decay Equations:
Identify the Decay Mode: The first step is to identify the decay mode from the decay equation. Common decay modes include alpha decay ($ \alpha $), beta-minus decay ($ \beta^- $), beta-plus decay ($ \beta^+ $), gamma decay ($ \gamma $), electron capture ($ \text{EC} $), and positron emission ($ \text{β}^+ $).
Determine the Daughter Nucleus: Next, determine the daughter nucleus that results from the decay process. The daughter nucleus is the resulting nucleus after the decay of the parent nucleus. It may have a different atomic number (Z) and mass number (A) compared to the parent nucleus.
Write the Decay Equation: Write the initial decay equation by placing the parent nucleus on the left-hand side and the daughter nucleus and emitted particle or radiation on the right-hand side. Include the symbols for the respective decay mode and the emitted particles.
Mass Number (A) Conservation: Ensure that the total mass number (A) is conserved on both sides of the equation. The sum of A on the left-hand side (parent nucleus) should be equal to the sum of A on the right-hand side (daughter nucleus and emitted particles).
Atomic Number (Z) Conservation: Ensure that the total atomic number (Z) is conserved on both sides of the equation. The sum of Z on the left-hand side (parent nucleus) should be equal to the sum of Z on the right-hand side (daughter nucleus and emitted particles).
Balance by Adjusting the Emitted Particles: If the equation is not balanced, adjust the number of emitted particles on the right-hand side to balance the equation. For example, if the equation involves the emission of two beta particles, make sure to include two beta particles on the right-hand side.
Verify the Balanced Equation: After making adjustments, verify that the equation is balanced by checking that the total mass number (A) and atomic number (Z) are equal on both sides.
Example Equations:
a. Alpha Decay:
b. Beta-Minus Decay:
c. Beta-Plus Decay:
d. Gamma Decay:
e. Electron Capture:
Conclusion: In this tutorial, we have learned how to balance radioactive decay equations correctly. By identifying the decay mode, determining the daughter nucleus, and ensuring the conservation of mass number (A) and atomic number (Z), we can accurately represent the decay process. Balancing these equations is essential in nuclear physics to understand the transformations of unstable atomic nuclei and their applications in radiometric dating, medical imaging, and nuclear energy.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - Predicting Types of Emission from Decay Equations
In this tutorial, we will learn how to predict the types of emission from radioactive decay equations. Radioactive decay is a natural process in which unstable atomic nuclei transform into more stable configurations by emitting various types of radiation. Understanding how to predict the types of emission is crucial in nuclear physics and has practical applications in radiometric dating, medical imaging, and nuclear energy. Let's delve into the key steps for predicting the types of emission from decay equations.
Identify the Decay Mode: The first step in predicting the type of emission is to identify the decay mode from the decay equation. Common decay modes include alpha decay ($ \alpha $), beta-minus decay ($ \beta^- $), beta-plus decay ($ \beta^+ $), gamma decay ($ \gamma $), electron capture ($ \text{EC} $), and positron emission ($ \text{β}^+ $).
Determine the Daughter Nucleus: Next, determine the daughter nucleus that results from the decay process. The daughter nucleus is the resulting nucleus after the decay of the parent nucleus. It may have a different atomic number (Z) and mass number (A) compared to the parent nucleus.
Identify the Emitted Particle or Radiation: Based on the decay mode, identify the emitted particle or radiation in the decay equation. Each decay mode involves the emission of specific particles or radiation:
a. Alpha Decay ($ \alpha $): In alpha decay, an alpha particle ($ ^4_2\text{He} $) is emitted from the parent nucleus. b. Beta-Minus Decay ($ \beta^- $): In beta-minus decay, a beta particle ($ ^0_{-1}\text{e} $) is emitted from the parent nucleus. c. Beta-Plus Decay ( ${\beta^+ }$ ): In beta-plus decay, a positron ($ ^0_{+1}\text{e} $) is emitted from the parent nucleus. d. Gamma Decay ($ \gamma $): In gamma decay, a gamma ray ($ \gamma $) is emitted from the parent nucleus. e. Electron Capture ($\text{EC} $): In electron capture, an electron is captured by the nucleus, resulting in the emission of a neutrino ($ \nu $) and a photon (X-ray or gamma ray).
Verify Mass and Atomic Number Conservation: Ensure that the decay equation satisfies the conservation of mass number (A) and atomic number (Z) on both sides of the equation. The sum of A and Z of the parent and daughter nuclei must be equal.
Example Equations:
a. Alpha Decay:
b. Beta-Minus Decay:
c. Beta-Plus Decay:
d. Gamma Decay:
e. Electron Capture:
In this tutorial, we have learned how to predict the types of emission from radioactive decay equations. By identifying the decay mode and determining the daughter nucleus, we can determine the emitted particle or radiation in the decay equation. Alpha decay emits an alpha particle ($ \alpha $), beta-minus decay emits a beta particle ($\beta^- $), beta-plus decay emits a positron ($\beta^+ $), gamma decay emits a gamma ray ($ \gamma $), and electron capture emits a neutrino ($ \nu $) and a photon (X-ray or gamma ray). Understanding how to predict the types of emission is essential for interpreting decay processes in nuclear physics and their applications in various scientific fields.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!
GCSE Physics Tutorial - Recognising Qualities in Radioactive Decay Equations
In this tutorial, we will explore the qualities present in radioactive decay equations. Radioactive decay equations represent the process by which unstable atomic nuclei transform into more stable configurations by emitting various types of radiation. Understanding the qualities of these equations is essential in nuclear physics and has practical applications in radiometric dating, medical imaging, and nuclear energy. Let's delve into the key qualities found in radioactive decay equations.
General Radioactive Decay Equation: The general form of a radioactive decay equation is written as follows: $$\text{Parent Nucleus} \rightarrow \text{Daughter Nucleus} + \text{Radiation} $$
Representation of Decay Mode: The decay mode is indicated by the type of radiation emitted in the equation. Common decay modes include alpha decay (${( \alpha )}$), beta-minus decay (${ \beta^- }$), beta-plus decay (${ \beta^+ }$), gamma decay (${ \gamma }$), electron capture (${ \text{EC} }$), and positron emission (${ \text{β}^+ }$).
Parent and Daughter Nuclei: The parent nucleus is the initial unstable radioactive isotope that undergoes decay. The daughter nucleus is the resulting nucleus after the decay process. The daughter nucleus may have a different atomic number (Z) and mass number (A) compared to the parent nucleus.
Mass Number Conservation: In a decay equation, the sum of the mass numbers (A) of the parent and daughter nuclei on both sides must be equal.
Atomic Number Conservation: The total atomic number (Z) of the parent and daughter nuclei on both sides of the equation must also be equal.
Emission of Radiation: The type of radiation emitted during decay is indicated in the equation. For example, alpha decay involves the emission of an alpha particle (${ \alpha }$), beta-minus decay emits a beta particle ($ {\beta^- }$), and gamma decay releases a gamma ray (${ \gamma }$).
Change in Atomic Number: In some decay modes, the atomic number (Z) changes, leading to a different element in the daughter nucleus. For example, beta-minus decay increases the atomic number by one, while beta-plus decay decreases the atomic number by one.
Change in Mass Number: In alpha decay, the mass number (A) of the parent nucleus decreases by four units, while the atomic number (Z) decreases by two.
Half-Life Representation: Decay equations do not explicitly include half-life values. Half-life is a separate property associated with each radioactive isotope, indicating the time it takes for half of the initial quantity of radioactive nuclei to decay.
Example Equations:
a. Alpha Decay:
b. Beta-Minus Decay:
c. Gamma Decay:
In this tutorial, we have explored the qualities found in radioactive decay equations. These equations represent the process of radioactive decay and are essential in understanding the transformations of unstable atomic nuclei into more stable configurations. The qualities include representation of decay mode, conservation of mass and atomic numbers, and the emission of radiation. Recognising these qualities is fundamental in nuclear physics and has diverse applications in radiometric dating, medical imaging, and nuclear energy.
Looking for a more dynamic learning experience?
Explore our engaging video lessons and interactive animations that GoPhysics has to offer – your gateway to an immersive physics education!